hostcosmic.blogg.se - Box and whisker plot outliers

#BOX AND WHISKER PLOT OUTLIERS HOW TO#

boxplot is also called Five number summary though Median, 1 st Quartile, 3 rd Quartile, Maximum and Minimum number can be visualized in a single diagram. What are the similarities and differences between Boxplot vs Bell Curve? AdvertisementĪmong various analytical techniques, boxplot is one of the frequently used technique for descriptive statistics.

#BOX AND WHISKER PLOT OUTLIERS HOW TO#

Interpretation of Box and Whisker Plot/ How to read Boxplot?.

Why Box plot is called Box and Whisker Plot?.

What is Boxplot or Box and Whisker Plot?.

Practice the concepts you have learned in this tutorial by using this So, then, any points that go beyond of the maximum size of the whiskers will be annotated in the box-plot and it will be considered an outlier. By definition, the box-plot limits the size of the whiskers to 1.5 times the interquartile range \((IQR)\) from the ends of the box (which are defined by \(Q_1\) and \(Q_3\). The most classical application for the box plot is for detecting outliers. The only raw values that would go in a boxplot would the outliers (if there is any). So in other words, the boxplot, unlike the histogram, presents a graph that represents a On the other hand, the boxplot provides summarized information about the quartiles and the 5-number summary, which tells you a lot about the relative position of the first and third quartile with respect to the median. Indeed, the histogram shows the raw shape of the distribution, based on the classes used to classify the possible values of the random variable.

One of the things about the box plot is that it provides information that is slightly different than the information provided by a histogram. , you can assess the degree of skewness of the distribution, and you can quickly scan regions have 25%, 50% and 75% of the total distribution.ĭifference between Box-plot and Histogram And the answer is simple: they give you a summarized depiction of the distribution of a sample by provided an schematic graph showing the relative position of the The main question people have is what do boxplots tell you. We conclude that the lower whisker is the minimum, and the top whisker is defined by \(Q_3 + 1.5 \times IQR = 55.25\). But now the maximum is 81, which exceeds \(Q_3 + 1.5 \times IQR = 55.25\). Observe that the minimum is 19, and it is greater than \(Q_1 - 1.5 \times IQR = 17.25\). The interquartile range in this case is \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). The following table shows the data in ascending order:

Similarly, if the maximum of the sample is less than \(Q_3 + 1.5 \times IQR\), then the top whisker is defined by the maximum. Otherwise, it is defined by \(Q_1 - 1.5 \times IQR\). So then, if the minimum of the sample is greater than \(Q_1 - 1.5 \times IQR\), then the lower whisker is defined by the minimum. This is provided that the size of the whisker is smaller than \(1.5 \times IQR\), where \(IQR\) is the interquartile range, and it is defined by \(IQR = Q_3 - Q_1\).

Now, for the whiskers there is a rule to follow: the bottom whisker is defined by the minimum of the sample, and the top whisker is defined by the maximum of the sample. The top line of the box is defined by the third quartile (\(Q_3\)). The middle line of the box is defined by the median (\(Q_2\)). The bottom line of the box is defined by the first quartile (\(Q_1\)). In the graph above you have an example of a how a boxplot looks like: You have the "box" and the whiskers. When the minimum or maximum are too extreme, the "trim" the whisker and we annotate the existence of an outlier.

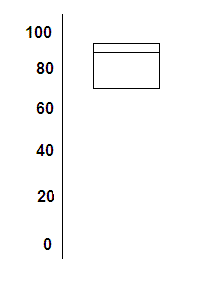
The Box and Whisker Plot, or also known as Box-plot, is a type of graphical depiction of a sample, that provides easy to see key features of the distribution of a sample.Ī box-and-whisker plot provides the median as well as the first and third quartiles in its "box", and the minimum and maximum in the "whisker".